Regionale Klimamodellierung Mit Methoden der regionalen Klimamodellierung werden globale Klimadaten für einzelne Regionen räumlich verfeinert.

Kurzfassung

Das Modell STARS (STatistical Analog Re-sampling Scheme) wurde zur Abschätzung zukünftiger klimatischer Entwicklungen im regionalen Skalenbereich entwickelt. Es ist ein statistisch basiertes Szenarienmodell, das generalisierte Informationen entweder aus globalen Zirkulationsmodellen oder aus eigenständigen Vorgaben mit Beobachtungsdaten über eine Reihe gekoppelter, statistischer Verfahren verknüpft. Dabei werden Witterungsabschnitte aus der Vergangenheit, die so auch unter den Entwicklungsvorgaben in einem Zukunftsszenarium auftreten können, derart neu zusammengesetzt, dass eine in Raum und Zeit physikalisch in sich konsistente Realisierung dieses Szenariums entsteht. Der extrem niedrige Rechenzeitaufwand ermöglicht es, eine große Anzahl von Realisierungen je Szenarium zu berechnen. Dadurch ist es möglich, eine statistisch gesicherte Aussage über die Unsicherheit des Modells zu treffen.

Hinweis: Dieses Modell wird gegenwärtig nicht mehr genutzt.

Die Modellstruktur

Die Fragestellung

Um eine Entwicklung zu beschreiben, verwendet das Verfahren als Prädiktor einen Trend, welcher sowohl aus Beobachtungs- bzw. Klimamodelldaten gewonnen werden kann. Der Trend entspricht also einer linearen Zu- oder Abnahme für einen ausgewählten meteorologischen Parameter in einem gegebenen Zeitraum. Diese Bezugsgröße beschreibt die langfristige Entwicklung und bezieht sich daher auf eine Glättung des gewählten meteorologischen Parameters. Dieser Parameter wird dabei so gewählt, dass er für das Klima der zu untersuchenden Region besonders charakteristisch ist. Diese Vorgabe ist selbstverständlich alles andere als vollständig bestimmend für die Simulation der klimatischen Entwicklung. Viele sehr unterschiedliche Simulationen, die alle einer solchen Vorgabe genügen, sind möglich – auch physikalisch unsinnige. Das Modell wurde deshalb so strukturiert, dass trotz dieser Unterbestimmtheit physikalisch sinnvolle Simulationen berechnet werden. Dabei musste abgesichert werden, dass

• die Kombination einzelner simulierter Variablen physikalisch plausibel bleibt (Ein Tag mit Niederschlag, aber ohne Bewölkung darf nicht auftauchen);
• die Jahresgänge in den simulierten Reihen erhalten bleiben (Die Sommer müssen wärmer als die Winter simuliert werden);
• die Persistenzen realistisch wiedergegeben werden (Einem heißen Tag darf kein Frosteinbruch folgen);
• die räumlichen Strukturen der meteorologischen Parameter erhalten bleiben (Ein warmer Frühlingstag in Berlin darf nicht von einem Frosteinbruch in Potsdam begleitet werden).

Auf Grund der Modellstruktur weisen beobachtete und simulierte Klimatologie zwangsläufig eine gewisse Mindestähnlichkeit auf – eine Eigenschaft des Verfahrens, die sich grundsätzlich bei statistischen Ansätzen findet. Der erste Modellansatz wurde bereits 1997 von Werner & Gerstengarbe veröffentlicht. Weitere Ergebnisse des auf dieser Basis entwickelten Regionalmodells finden sich unter anderem bei Gerstengarbe et al. 2003 und Gerstengarbe & Werner 2005. 2007 wurde eine von Orlowsky weiterentwickelte Version veröffentlicht, die die Grundlage dieser Modellbeschreibung lieferte [1]. (Weiterführende Informationen bzw. Anwendungen des Modells finden sich in der Literaturliste.)

[1] Die vorliegende Modellbeschreibung enthält Textbausteine aus der Dissertation von B. Orlowsky, die so nicht besser hätten formuliert werden können.


Die Herangehensweise für einzelne Stationen

Um die oben aufgeführten Bedingungen sicherzustellen, muss eine wichtige Annahme getroffen werden: Zeitliche Abschnitte der Beobachtungsreihen können während der Simulationsperiode erneut oder zumindest in sehr ähnlicher Weise auftreten. Unter dieser Voraussetzung werden in dem Modell Zeitabschnitte der Simulationsreihen aus Zeitabschnitten der Beobachtungsreihen unter Einhaltung des vorgegebenen Trends neu zusammengesetzt (vergleiche Abbildung 1).

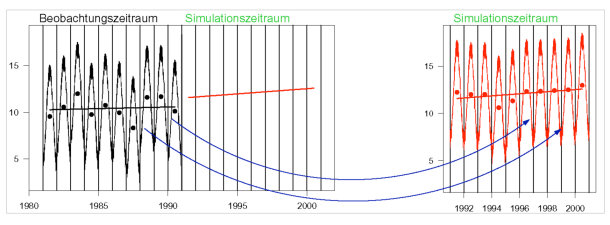
Abb. 1: Illustration der Fragestellung und des Ansatzes: Gegeben ist eine Beobachtungsreihe (dargestellt durch eine synthetische Temperaturreihe in schwarz) und eine vorgegebene Regressionsgerade (rot) für den Simulationszeitraum (links). Gesucht ist eine simulierte Reihe (ebenfalls rot), die der Vorgabe genügt und aus Abschnitten der Beobachtungsreihe zusammengesetzt ist (rechts). Die Punkte zeigen jeweils die Jahresmittel an, auf die sich die Regressionsvorgabe bezieht.

Die modellmäßige Umsetzung der Fragestellung ist in Abbildung 2 beispielhaft für eine/n Station/Gitterpunkt dargestellt. Sie besteht aus einem „INPUT“-Teil und zwei Verfahrensschritten, die auf unterschiedlichen Zeitskalen arbeiten: der erste auf der Skala von Jahren (in der Abbildung grau hinterlegt), der zweite auf der Skala von 12-Tages-Blöcken (weiß hinterlegt).
 Bildvergrößerung

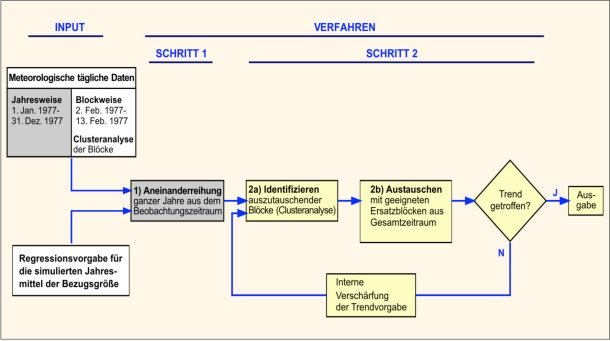
Abb. 2: Zusammenfassende Gesamtdarstellung des Verfahrens für eine einzelne Station mit der Temperatur als Bezugsgröße

 Bildvergrößerung

„INPUT“-Teil

Die Beobachtungsreihe wird zu Beginn einmal nach Jahren (erstes Beobachtungsjahr vom 1. Januar bis 31. Dezember, zweites Beobachtungsjahr vom …, usw.) und einmal nach gleitenden 12-Tages-Blöcken (1. bis 12. Januar – erstes Beobachtungsjahr, 13. bis 24. Januar, …, 20. bis 31. Dezember – letztes Beobachtungsjahr). unterteilt. Sowohl Jahre als auch Blöcke sind mit einer Liste von Kalenderdaten und ihren dazugehörigen Beobachtungen verbunden.
Die Blöcke n der Bezugsgröße werden durch eine Cluster-Analyse (Werner & Gerstengarbe 1997; Gerstengarbe et al., 1999) klassifiziert, die jeweils ähnliche Blöcke in Klassen zusammenfasst.

Verfahren – Schritt 1

Im ersten Schritt werden die Jahresabschnitte der Beobachtungsreihe mit Hilfe einer Monte-Carlo-Simulation neu aneinandergereiht. Ziel ist es, durch die Neuanordnung möglichst nahe an den vorgegebenen Regressionsparameter (Trend) zu gelangen. Dazu wird eine große Stichprobe von zufälligen Reihungen jährlicher Abschnitte jeweils in der Länge des Simulationszeitraums erzeugt. Für jede dieser zufälligen Reihungen wird der Trend der Bezugsgröße bestimmt und letztlich diejenige Simulation ausgewählt, die der vorgegebenen Regressionsgeraden am nächsten kommt. Trotzdem muss in der Regel diese erste Näherung nachgebessert werden, um die Vorgabe bis auf ein definiertes ε möglichst exakt zu erreichen.

Verfahren – Schritt 2

Im zweiten Schritt erfolgt die Optimierung der Anpassung an die Regressionsgerade. Hierzu werden die 12-Tages-Blöcke eingesetzt. Zuerst wird die sich aus der ersten Näherung ergebende Reihe Block für Block durchgesehen und für jeden Block entschieden, ob er, bis auf ein definiertes ε, aus der ersten Näherung übernommen werden kann, oder nicht. Kann der jeweilige Block das Kriterium nicht erfüllen, muss ein passender Ersatz aus den Blöcken des Beobachtungszeitraums gesucht werden. Dieser Ersatzblock wird aus den Clustern des INPUT-Bereichs so ausgewählt, dass sich einerseits physikalisch plausible Witterungsabfolgen ergeben, andererseits die auf diese Weise schrittweise entstehende Reihe der Bezugsgröße der Regressionsvorgabe genügt.

Hinter dem Vorgehen des zweiten Schritts stehen folgende Überlegungen:

• Die Verwendung von Blöcken der Länge von 12 Tagen garantiert realistische Witterungsabfolgen innerhalb der Blöcke, da sie ja einem tatsächlich beobachteten Witterungsgeschehen entstammen.
• Desweiteren sichert die Länge von 12 Tagen die typischen Erhaltungsneigungen von Größen wie Temperatur, Luftdruck und Niederschlag an Stationen des Untersuchungsgebietes ab.
• Da ein Teil der Blöcke aus der ersten Näherung übernommen wird, bleibt ein „Grundgerüst“ der beobachteten Jahre einschließlich des Jahresganges erhalten. Damit ist eine physikalisch plausible Witterungsabfolge innerhalb der einzelnen Jahre garantiert.

Die Herangehensweise für mehrere Stationen

Die beschriebene Herangehensweise für eine einzelne Station lässt sich unverändert auf Simulationen für beliebig viele Stationen übertragen. Der wesentliche Unterschied besteht einzig darin, dass die Abläufe lediglich in einem höherdimensionalen Raum stattfinden. Das heißt, dass man jetzt die Regressionsvorgaben (Trends) für jede der Stationen die man betrachten will, benötigt. Ebenso wird die Cluster-Analyse genutzt, um ähnliche Blöcke aller Stationen in jeweils einem Cluster zusammenzufassen. Damit enthält ein Jahr der Beobachtungsperiode neben den Kalenderdaten die Beobachtungen aller Stationen der Untersuchungsregion, genauso wie die Blöcke. Diese Unterschiede in der Dimensionalität sind die einzigen, die zwischen der Betrachtungsweise für eine Station und beliebig vielen Stationen bestehen. Je nach Stationsdichte und klimatischer Heterogenität des Untersuchungsgebiets kann man, um Rechenzeit zu sparen, die Dimensionalität deutlich verringern. Hier bietet sich wieder die Cluster-Analyse an. Diesmal wird sie allerdings dazu genutzt, alle Stationen mit einer ähnlichen Struktur der Bezugsgröße, in jeweils einer Klasse zusammenzufassen. Für jede der Klassen wird nun die Station, die dem Clusterzentrum am nächsten liegt, als Repräsentantin gewählt. Nur diese repräsentativen Stationen bekommen dann die Regressionsparameter vorgegeben und bringen ihre Beobachtungsreihen in das Verfahren ein. Mit Hilfe der Daten der repräsentativen Stationen lassen sich dann auch die Simulationsreihen der nicht verwendeten Stationen konstruieren, obwohl diese zur Auswahl der verwendeten Blöcke nichts beitragen. Wesentlich dabei ist, dass auf diese Weise die räumliche Struktur des momentanen Zustands der Atmosphäre für das gesamte Untersuchungsgebiet erhalten bleibt.

Die aktuellen STARS Szenarien für Deutschland (Gerstengarbe et al. 2015) sind im Internet Portal www.klimafolgenonline.com abrufbar.
 www.klimafolgenonline.com

Kritische Anmerkungen

Unterscheidet sich die Temperaturvorgabe deutlich vom gegenwärtigen Klimazustand der Beobachtungsperiode, offenbaren sich deutliche Schwächen des Modellansatzes. Vor allem in den Sommermonaten werden häufiger Witterungsepisoden gezogen, die in der Vergangenheit heiß und trocken gewesen sind. Dies führt zu Fehleinschätzungen zukünftiger klimatischer Entwicklungen hinsichtlich der Wasserverfügbarkeit im Vergleich zu Klimaänderungssignalen in dynamischen Regionalmodellen. Auch weisen die Realisierungen der durch STARS generierten Simulationen starke Ähnlichkeiten auf und stellen somit nicht die vollständige Bandbreite der möglichen Klimaentwicklungen dar (Wechsung & Wechsung 2014, 2015).

Die Anwendung des Modellansatzes in der nahen Zukunft (10-20 Jahre) ist hingegen weniger kritisch und zugleich ein Vorteil, um auch unabhängig von Vorgaben aus Klimamodellen auf der Basis von beobachteten Trends mögliche Entwicklungen fortzuschreiben. Mit saisonalen Trendvorgaben für mehrere Variablen können somit realistischere Entwicklungsverläufe generiert werden.