Regionale Klimamodellierung Mit Methoden der regionalen Klimamodellierung werden globale Klimadaten für einzelne Regionen räumlich verfeinert.

HIRHAM-NAOSIM

Das regionale Klimamodell HIRHAM–NAOSIM (Dorn et al., 2019) ist ein gekoppeltes Atmosphären-Ozean-Meereis-Modell für die Arktis. Es besteht aus dem regionalen atmosphärischen Klimamodell HIRHAM5 (Christensen et al., 2007) und dem regionalen Ozean-Meereis-Modell NAOSIM (Köberle und Gerdes, 2003; Fieg et al., 2010). Für die Kopplung der beiden Modellkomponenten wird die Kopplungssoftware YAC (Hanke et al., 2016) verwendet.

Modellkomponenten

HIRHAM5 ist ein regionales atmosphärisches Klimamodell, welches auf die Arktis angewendet wird. HIRHAM5 besteht aus dem dynamischen Kern des numerischen Wettervorhersagemodells HIRLAM-7.0 (Undén et al., 2002) und den physikalischen Parametrisierungen des atmosphärischen allgemeinen Zirkulationsmodells ECHAM-5.4 (Roeckner et al., 2003). Für die Anwendung auf die Arktis wurden einige dieser Parametrisierungen an die besonderen Klimabedingungen der Arktis angepasst bzw. durch alternative Parametrisierungen ergänzt. Dies betrifft zum Beispiel die Parametrisierung der Meereis-Albedo (Køltzow, 2007; Jäkel et al., 2019), der Wolkenbedeckung (Klaus et al., 2016) und der atmosphärischen Grenzschicht (Lüpkes und Gryanik, 2015; Gryanik und Lüpkes, 2018).

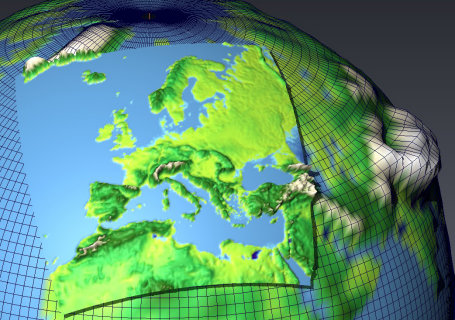
Das Modellgebiet umfasst die gesamte Arktis nördlich von etwa 60⁰ N (Abbildung 1) und ist durch konkrete Breiten- und Längengrade eines rotierten sphärischen Koordinatensystems definiert, dessen Nordpol bei 180⁰ O auf dem geografischen Äquator liegt [1]. HIRHAM5 wird in der aktuellen Konfiguration mit einer horizontalen Auflösung von 0.25⁰ (etwa 27 km) und einem Zeitschritt von 600 s (10 Minuten) gerechnet. Standardmäßig verwendet das Modell 40 vertikale Schichten von etwa 10 m Höhe über Grund bis in eine Höhe, bei der der Luftdruck 10 hPa beträgt (etwa 37 km über dem Meeresspiegel), wobei der unterste Kilometer der Atmosphäre durch 10 vertikale Schichten dargestellt wird. Die prognostischen Größen sind Bodenluftdruck, die beiden horizontalen Windkomponenten, Lufttemperatur, spezifische Feuchte, Wolkenwasser und Wolkeneis. Zudem werden etliche diagnostische Größen (z. B. Strahlungsflüsse, Wolkenbedeckung, Niederschlagsart und -menge u.v.m.) im Modell bestimmt.

NAOSIM ist ein Ozean–Meereismodell für den nördlichen Nordatlantik und den Arktischen Ozean (North Atlantic/Arctic Ocean-Sea Ice Model). Die ozeanische Modellkomponente basiert auf dem Modularen Ozeanmodell MOM-2 (Pacanowski, 1996) und berechnet die dreidimensionale Zirkulation des Ozeans. Prognostischen Größen sind die beiden horizontalen Komponenten der Ozeanströmung, die Temperatur und der Salzgehalt. Die Meereiskomponente basiert auf dem dynamisch-thermodynamischen Meereismodell von Hibler (1979) mit Erweiterungen von Harder et al. (1998). Prognostischen Größen sind die Eiskonzentration [2], die Eisdicke, die Schneedicke und das Alter des Eises. Die Eisdriftgeschwindigkeit hingegen wird diagnostisch aus der Impulsbilanz unter Vernachlässigung expliziter Zeitabhängigkeit bestimmt.

Das Modellgebiet umfasst den gesamten Arktischen Ozean, das Europäische Nordmeer und den nördlichen Nordatlantik mit einer südlichen Modellgrenze bei etwa 50⁰ N (Abbildung 1). NAOSIM verwendet ein rotiertes sphärisches Koordinatensystem, dessen Nordpol bei 60⁰ O auf dem geografischen Äquator liegt. Das Modell hat maximal 50 vertikale Schichten im Ozean (je nach Tiefe des Ozeans) und wird mit einer horizontalen Auflösung von 1/12⁰ (etwa 9 km) und einem Zeitschritt von 360 s (6 Minuten) gerechnet.

Modellkopplung

Das Atmosphärenmodell berechnet die Flüsse von Impuls 𝜏⃗ (Windschub), Wärme Q (kurz- und langwellige Strahlung, fühlbarer und latenter Wärmefluss) und Feuchte F (Niederschlag, Verdunstung) getrennt für offenes Wasser und für den mit Eis bedeckten Teil jeder Gitterbox (gekennzeichnet durch Indizes o und i in Abbildung 2). Diese Flüsse werden ans Ozean–Meereismodell übergeben und gehen dort direkt in die Bilanzgleichungen von Impuls, Wärme und Süßwasser (bzw. Schnee) als oberer Randantrieb ein. Im Gegenzug liefert das Ozean–Meereismodell die Zustandsgrößen Meeresoberflächentemperatur Tₒ, Gefriertemperatur der Meeresoberfläche (als Funktion des Salzgehalts) T_f, Eiskonzentration A, Eisdicke hᵢ und Schneedicke hₛ an das Atmosphärenmodell als Randbedingungen zur Berechnung der Flüsse, die den vertikalen Austausch von Impuls, Wärme und Feuchte am unteren Rand der Atmosphäre beschreiben (siehe Abbildung 2).

Die Kopplung zwischen HIRHAM5 und NAOSIM wird in der aktuellen Modellkonfiguration jede Stunde durchgeführt. Da HIRHAM5 und NAOSIM unterschiedlich ausgerichtete Modellgitter (siehe Abbildung 1) mit unterschiedlicher horizontaler Auflösung haben, müssen die Austauschgrößen vom einen zum anderen Gitter interpoliert werden. Vor der Interpolation müssen die Vektoren 𝜏⃗ᵢ und 𝜏⃗ₒ vom rotierten sphärischen Koordinatensystem des HIRHAM5 ins rotierte sphärische Koordinatensystem des NAOSIM transformiert werden. Da beide Modellgitter den geografischen Nordpol als Koordinate (0,0) gemein haben, ist für die Transformation der Vektoren lediglich eine Drehung um 120⁰ an der Polachse notwendig.

Die Gitterinterpolation wird anschließend von der Kopplungssoftware YAC (Hanke et al., 2016) bewerkstelligt, wobei vorrangig eine konservative Interpolation 1. Ordnung verwendet wird, die Erhaltungseigenschaften garantiert (Jones, 1999). Für Gitterzellen, die aufgrund unterschiedlicher Land-Meer-Verteilung der beiden Modellgitter keine überlappenden Gitterzellen besitzen, werden die Werte der zwei am nächsten benachbarten Gitterzellen zur Interpolation verwendet. Die Ozean-Gitterzellen außerhalb des Überschneidungsgebiets der beiden Modellkomponenten (d. h. außerhalb des gelb markierten Bereichs in Abbildung 1) werden genauso wie in ungekoppelten Modellsimulationen behandelt. Das bedeutet, dass dort die benötigten unteren bzw. oberen Randbedingungen modellintern aus Reanalysedaten [3] bestimmt werden, die auch für den seitlichen Randantrieb des Modells verwendet werden.

Anwendung des gekoppelten Modells

Das gekoppelte regionale Klimamodell HIRHAM–NAOSIM dient vor allem der Untersuchung von Wechselwirkungen und Rückkopplungen zwischen Atmosphäre und Meereis und deren Bedeutung für die in den letzten Jahren beobachtete Abnahme der arktischen Meereisbedeckung. Zum einen dient das Modell als Testumgebung für verbesserte Parametrisierungen [4], die mit den Wechselwirkungsprozessen in Verbindung stehen, zum anderen wird es für Fallstudien eingesetzt, um besser zu verstehen, welche Wechselwirkungen zwischen Atmosphäre und Meereis zu relevanten Änderungen im arktischen Klimasystem führen. Zum Beispiel wurde der Einfluss mehrerer, aufeinanderfolgender Zyklonen auf die Änderungen der Meereiskonzentration und Meereisdicke in einer Fallstudie von Aue et al. (2023) untersucht. In dieser Studie zeigte sich, dass dynamische Prozesse, wie erhöhte Eisdrift und Eisdeformation, infolge des Durchzugs der Zyklonen einen dominanten Einfluss auf regionale Änderungen des Meereises haben. Diese dynamisch bedingten Änderungen des Meereises haben wiederum Einfluss auf das thermodynamische Eiswachstum im Anschluss an den Durchzug der Zyklonen.

Dass eine realitätsnahe Simulation der atmosphärischen Zirkulation (d. h. des Bodenluftdruckfeldes inklusive der damit in Verbindung stehenden Temperaturverteilung und Wolkenbedeckung) während der Sommermonate eine notwendige Bedingung für die realistische Simulation des sommerlichen Meereisrückgangs ist, konnte bereits von Dorn et al. (2012) gezeigt werden. Voraussetzung ist allerdings, dass einerseits die Meereisdickenverteilung am Beginn der Schmelzperiode hinreichend realistisch wiedergegeben wird und andererseits die Eis-Albedo-Rückkopplung, die als selbstverstärkender Rückkopplungsprozess wesentlich für die Geschwindigkeit der Eisschmelze ist, realistisch vom Modell simuliert wird.

Um die Eis-Albedo-Rückkopplung realistisch zu simulieren, ist es erforderlich die Albedo [5] möglichst genau zu parametrisieren. Diesbezüglich konnten in den letzten Jahren bereits einige Verbesserungen erzielt werden (Dorn et al., 2009; Jäkel et al., 2019; Foth et al., 2023). Wesentlich schwieriger ist es, die atmosphärische Zirkulation und die Meereisdickenverteilung realistisch zu simulieren. Dies ist darin begründet, dass die Atmosphäre ein nichtlineares dynamisches System ist [6], das zudem mit dem Meereis in nichtlinearer Weise wechselwirkt. Durch die erhöhte Nichtlinearität des gekoppelten Modellsystems gegenüber einem reinen Atmosphärenmodell ist auch die interne Modellvariabilität im gekoppelten Modell stärker ausgeprägt.

Als Beispiel zeigt Abbildung 3 die Unterschiede des mittleren Luftdrucks in Meeresniveau zwischen den Perioden 2005–2021 und 1989–2004 von 4 exemplarisch ausgewählten Simulationen eines 10 Mitglieder umfassenden Ensembles von HIRHAM–NAOSIM-Simulationen. Die 10 Simulationen wurden jeweils an den seitlichen Rändern der Atmosphäre mit Daten der ERA5-Reanalyse (Hersbach et al., 2020) bzw. an den seitlichen Rändern des Ozeans mit Daten der ORAS5-Reanalyse (Zuo et al., 2019) angetrieben und wurden jeweils mit ERA5-Reanalysedaten (Atmosphäre) bzw. ORAS5-Reanalysedaten (Ozean und Meereis) initialisiert, starteten aber sukzessive um ein Jahr versetzt („run01” im Januar 1979 bis „run10” im Januar 1988). Die 10 Simulationen umfassen alle die Periode 1989–2021, haben aber einen unterschiedlich langen Vorlauf von 1 (run10) bis 10 Jahren (run01), sodass sich ihr virtueller Anfangszustand am 1. Januar 1989 unterscheidet.

Im Vergleich zur Periode 1989–2004 zeigen die 4 Simulationen für die Periode 2005–2021 zwar alle eine Luftdruckzunahme über Grönland, dem nördlichen Nordatlantik und Nordeuropa, aber völlig unterschiedliche Luftdruckänderungen in der inneren Arktis. Insbesondere im Bereich der nördlichen Barents- und Karasee, wo die ERA5-Reanalyse, die in Bezug auf den Luftdruck als Beobachtung interpretiert werden kann, eine Luftdruckabnahme zeigt, zeigen einige Simulationen eine deutliche Luftdruckzunahme. Auch wenn alle Simulationen am seitlichen Rand mit Daten der ERA5-Reanalyse angetrieben wurden, ist doch keine einzige in der Lage, die beobachteten Luftdruckänderungen in der inneren Arktis zu reproduzieren.

Die Unterschiede in den simulierten Luftdruckänderungen spiegeln sich auch in den Änderungen der simulierten mittleren Eisdicke zwischen den Perioden 2005–2021 und 1989–2004 wider (Abbildung 4). Die 4 Simulationen zeigen deutlich unterschiedliche Muster der Eisdickenänderung, die zumindest teilweise mit den unterschiedlichen Luftdruckänderungen in Verbindung stehen dürften, wie frühere Untersuchungen von Rinke et al. (2013, 2019) aufgezeigt haben. In Bezug auf die Eisdickenänderung zeigen allerdings auch verschiedene Reanalysen (ORAS5 gegenüber PIOMAS (Schweiger et al., 2011)) kein einheitliches Änderungsmuster. Dies ist darin begründet, dass die Eisdicke in Reanalysen auf Modellrechnungen beruht, da aufgrund fehlender bzw. lückenhafter Beobachtungen der Eisdicke lediglich beobachtete Eiskonzentrationen und Meeresoberflächentemperaturen in die Reanalysen assimiliert werden. Dennoch lässt sich feststellen, dass die Eisdickenänderung in HIRHAM–NAOSIM durchweg zwar das richtige Vorzeichen hat (Eisabnahme), in den meisten Regionen aber etwas geringer ist als in den Reanalysen. Dies deutet darauf hin, dass Rückkopplungsprozesse, die für die realen arktischen Klimaänderungen verantwortlich sind, eventuell noch nicht hinreichend im Modell dargestellt werden.

Die Unterschiede zwischen den einzelnen HIRHAM–NAOSIM-Simulationen sind ein Ausdruck interner Modellvariabilität, wie sie für nichtlineare dynamische Systeme typisch ist. Insbesondere in gekoppelten Modellen des arktischen Klimasystems spielt die intern erzeugte Variabilität eine wichtige Rolle (siehe z. B. Döscher et al., 2010; Dorn et al., 2012). Sie stellt einen limitierenden Faktor für die Reproduktion des beobachteten Zustands des arktischen Klimasystems dar. Andererseits sind systematische Unterschiede zwischen Modellsimulation und Beobachtung (Reanalyse) oft ein Ausdruck einer unzureichend realistischen Darstellung der für das arktische Klimasystem relevanten physikalischen Prozesse.

Für Fallstudien oder Sensitivitätsstudien ist es in der Regel sinnvoll, die durch interne Modellvariabilität hervorgerufenen Abweichungen der simulierten atmosphärischen Zirkulation gegenüber den Beobachtungen zu unterdrücken. Zu diesem Zweck bietet HIRHAM5 die Option des Nudgings an Reanalysedaten [7]. Mit Hilfe des Nudgings kann die großskalige atmosphärische Zirkulation der Reanalysedaten reproduziert werden, sodass der Unterschied zwischen Modellsimulation und Beobachtung im Wesentlichen nur noch eine Folge einer unzureichenden Parametrisierung physikalischer Prozesse ist. Nudging wurde zum Beispiel in den Fall- bzw. Sensitivitätsstudien von Aue et al. (2023) und Foth et al. (2023) verwendet und ist eine notwendige Voraussetzung für den direkten Vergleich von Modelldaten mit Beobachtungen, was ansonsten nur anhand des Vergleichs von Klimastatistiken möglich wäre und lange Simulationen und/oder große Ensemble erfordern würde.

Literatur

Aue, L., Röntgen, L., Dorn, W., Uotila, P., Vihma, T., Spreen, G., und Rinke, A. (2023): Impact of three intense winter cyclones on the sea ice cover in the Barents Sea: A case study with a coupled regional climate model, Front. Earth Sci., 11, 1112467, doi:10.3389/feart.2023.1112467.

Christensen, O. B., Drews, M., Christensen, J. H., Dethloff, K., Ketelsen, K., Hebestadt, I., und Rinke, A. (2007): The HIRHAM Regional Climate Model Version 5 (β), DMI Technical Report 06-17, Danish Meteorological Institute, Copenhagen, Denmark, http://www.dmi.dk/fileadmin/Rapporter/TR/tr06-17.pdf.

Dorn, W., Dethloff, K., und Rinke, A. (2009): Improved simulation of feedbacks between atmosphere and sea ice over the Arctic Ocean in a coupled regional climate model, Ocean Model., 29, 103–114, doi:10.1016/j.ocemod.2009.03.010.

Dorn, W., Dethloff, K., und Rinke, A. (2012): Limitations of a coupled regional climate model in the reproduction of the observed Arctic sea-ice retreat, Cryosphere, 6, 985–998, doi:10.5194/tc-6-985-2012.

Dorn, W., Rinke, A., Köberle, C., Dethloff, K., und Gerdes, R. (2019): Evaluation of the sea-ice simulation in the upgraded version of the coupled regional atmosphere-ocean-sea ice model HIRHAM–NAOSIM 2.0, Atmosphere, 10, 431, doi:10.3390/atmos10080431.

Döscher, R., Wyser, K., Meier, H. E. M., Qian, M., und Redler, R. (2010): Quantifying Arctic contributions to climate predictability in a regional coupled ocean-ice-atmosphere model, Clim. Dyn., 34, 1157–1176, doi:10.1007/s00382-009-0567-y.

Fieg, K., Gerdes, R., Fahrbach, E., Beszczynska-Möller, A., und Schauer, U. (2010): Simulation of oceanic volume transports through Fram Strait 1995–2005, Ocean Dyn., 60, 491–502, doi:10.1007/s10236-010-0263-9.

Foth, L., Dorn, W., Rinke, A., Jäkel, E., und Niehaus, H. (2023): On the importance to consider the cloud dependence in parameterizing the albedo of snow on sea ice, EGUsphere [preprint], doi:10.5194/egusphere-2023-634.

Gryanik, V. M. und Lüpkes, C. (2018): An efficient non-iterative bulk parametrization of surface fluxes for stable atmospheric conditions over polar sea-ice, Bound. Layer Meteorol., 166, 301–325, doi:10.1007/s10546-017-0302-x.

Hanke, M., Redler, R., Holfeld, T., und Yastremsky, M. (2016): YAC 1.2.0: new aspects for coupling software in Earth system modelling, Geosci. Model Dev., 9, 2755–2769, doi:10.5194/gmd-9-2755-2016.

Harder, M., Lemke, P., und Hilmer, M. (1998): Simulation of sea ice transport through Fram Strait: Natural variability and sensitivity to forcing, J. Geophys. Res., 103, 5595–5606, doi:10.1029/97JC02472.

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., Chiara, G. D., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., und Thépaut, J.-N. (2020): The ERA5 global reanalysis, Q. J. R. Meteorol. Soc., 146, 1999–2049, doi:10.1002/qj.3803.

Hibler, III, W. D. (1979): A dynamic thermodynamic sea ice model, J. Phys. Oceanogr., 9, 815–846, doi:10.1175/1520-0485(1979)009<0815:ADTSIM>2.0.CO;2.

Jäkel, E., Stapf, J., Wendisch, M., Nicolaus, M., Dorn, W., und Rinke, A. (2019): Validation of the sea ice surface albedo scheme of the regional climate model HIRHAM–NAOSIM using aircraft measurements during the ACLOUD/PASCAL campaigns, Cryosphere, 13, 1695– 1708, doi:10.5194/tc-13-1695-2019.

Jones, P. W. (1999): First- and second-order conservative remapping schemes for grids in spherical coordinates, Mon. Weather Rev., 127, 2204–2210, doi:10.1175/1520-0493(1999)127<2204:FASOCR>2.0.CO;2.

Klaus, D., Dethloff, K., Dorn, W., Rinke, A., und Wu, D. L. (2016): New insight of Arctic cloud parameterization from regional climate model simulations, satellite-based, and drifting station data, Geophys. Res. Lett., 43, 5450–5459, doi:10.1002/2015GL067530.

Köberle, C. und Gerdes, R. (2003): Mechanisms determining the variability of Arctic sea ice conditions and export, J. Clim., 16, 2843–2858, doi:10.1175/1520-0442(2003)016<2843:MDTVOA>2.0.CO;2.

Køltzow, M. (2007): The effect of a new snow and sea ice albedo scheme on regional climate model simulations, J. Geophys. Res., 112, D07110, doi:10.1029/2006JD007693.

Lüpkes, C. und Gryanik, V. M. (2015): A stability-dependent parametrization of transfer coefficients for momentum and heat over polar sea ice to be used in climate models, J. Geophys. Res. Atmos., 120, 552–581, doi:10.1002/2014JD022418.

Pacanowski, R. C. (1996): MOM 2 Documentation, User’s Guide and Reference Manual, GFDL Ocean Technical Report 3.2, Geophysical Fluid Dynamics Laboratory, Princeton, NJ, USA, https://www.gfdl.noaa.gov/mom-ocean-model/.

Rinke, A., Dethloff, K., Dorn, W., Handorf, D., und Moore, J. C. (2013): Simulated Arctic atmospheric feedbacks associated with late summer sea ice anomalies, J. Geophys. Res. Atmos., 118, 7698–7714, doi:10.1002/jgrd.50584.

Rinke, A., Knudsen, E. M., Mewes, D., Dorn, W., Handorf, D., Dethloff, K., und Moore, J. C. (2019): Arctic summer sea ice melt and related atmospheric conditions in coupled regional climate model simulations and observations, J. Geophys. Res. Atmos., 124, 6027–6039, doi:10.1029/2018JD030207.

Roeckner, E., Bäuml, G., Bonaventura, L., Brokopf, R., Esch, M., Giorgetta, M., Hagemann, S., Kirchner, I., Kornblueh, L., Manzini, E., Rhodin, A., Schlese, U., Schulzweida, U., und Tompkins, A. (2003): The atmospheric general circulation model ECHAM5 – Part I: Model description, MPI Report 349, Max Planck Institute for Meteorology, Hamburg, Germany, https://hdl.handle.net/11858/00-001M-0000-0012-0144-5.

Schweiger, A., Lindsay, R., Zhang, J., Steele, M., Stern, H., und Kwok, R. (2011): Uncertainty in modeled Arctic sea ice volume, J. Geophys. Res., 116, C00D06, doi:10.1029/2011JC007084.

Undén, P., Rontu, L., Järvinen, H., Lynch, P., Calvo, J., Cats, G., Cuxart, J., Eerola, K., Fortelius, C., Garcia-Moya, J. A., Jones, C., Lenderlink, G., McDonald, A., McGrath, R., Navascues, B., Nielsen, N. W., Ødegaard, V., Rodriguez, E., Rummukainen, M., Rõõm, R., Sattler, K., Sass, B. H., Savijärvi, H., Schreur, B. W., Sigg, R., The, H., und Tijm, A. (2002): HIRLAM-5 Scientific Documentation, HIRLAM-5 Project Report, Swedish Meteorological and Hydrological Institute, Norrköping, Sweden, http://hirlam.org/index.php/hirlam-programme-53/general-model-description/synoptic-scale-hirlam.

Zuo, H., Balmaseda, M. A., Tietsche, S., Mogensen, K., und Mayer, M. (2019): The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: a description of the system and assessment, Ocean Sci., 15, 779–808, doi:10.5194/os-15-779-2019.

Fußnoten

[1] Durch die Verwendung eines rotierten sphärischen Koordinatensystems sind die Gitterpunkte annährend äquidistant, sodass numerische Probleme, die bei Verwendung eines regulären geografischen Gitters im Bereich der Pole auftreten würden, vermieden werden.

[2] Die Eiskonzentration gibt den Anteil der eisbedeckten Fläche pro Gitterzelle an und kann zwischen 0 % (komplett eisfreie Gitterzelle) und 100 % (geschlossene Eisbedeckung in der Gitterzelle) schwanken.

[3] Reanalysen sind Datensätze, die unter Verwendung von Wettervorhersagemodellen und Assimilation von Beobachtungsdaten erstellt werden. Sie stellen eine dreidimensional konsistente Beschreibung des atmosphärischen Zustandes dar, der dem beobachteten Zustand sehr nahekommt.

[4] Unter Parametrisierung versteht man die Beschreibung der Effekte von kleinskaligen (d. h. unterhalb der Modellmaschenweite stattfindenden) Prozessen auf die Modellgrößen.

[5] Die Albedo ist ein Maß für das Rückstrahlvermögen von diffus reflektierenden, also nicht selbst leuchtenden Oberflächen, und entspricht dem Verhältnis von rückgestrahlter zu einfallender Strahlung.

[6] Ein nichtlineares dynamisches System ist ein System, dessen zeitliche Entwicklung langfristig nicht vorhersagbar ist, obwohl die zugrundeliegenden Gleichungen eigentlich deterministisch sind. Beliebig kleine Änderungen der Anfangsbedingungen des Systems können im Langzeitverhalten zu völlig unterschiedlichen Ergebnissen führen.

[7] Nudging, oder Newton’sche Relaxation, ist eine Methode der Datenassimilation, bei der die prognostischen Modellvariablen in Richtung der beobachteten Werte relaxiert werden. Dies geschieht, indem den prognostischen Gleichungen ein zusätzlicher Term hinzugefügt wird, der die mit dem entsprechenden Relaxationskoeffizienten gewichtete Differenz zwischen beobachteten und berechneten Wert der Variable enthält.