REMO
Entwicklung
Das regionale Klimamodell REMO (Jacob & Podzun 1997, Jacob 2001) ist ein dreidimensionales atmosphärisches Zirkulationsmodell, das ursprünglich aus einem numerischen Wettervorhersagemodell des Deutschen Wetterdienstes - dem Europamodell EM (Majewski 1991) - entwickelt wurde. Zudem wurden die physikalischen Parametrisierungen des globalen Zirkulationsmodells ECHAM4 (Roeckner et al. 1996) implementiert. Diese Kombination von dynamischem Kern aus dem Wettervorhersagemodell und physikalischen Prozessen aus dem Globalmodell hat sich in der Simulation des regionalen Klimas bewährt und stellte den Ausgangspunkt für die weitere Entwicklung von einem regionalen Atmosphärenmodell zu einem dreidimensionalen Ausschnittsmodell des Systems Atmosphäre - Ozean - Land dar.
REMO-Homepage
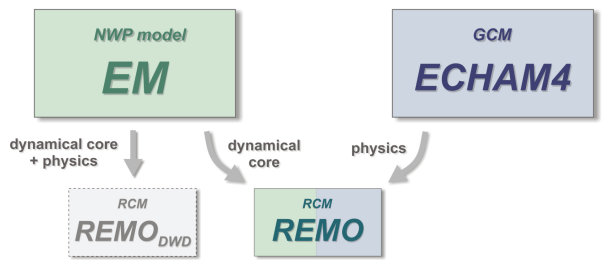
Abbildung 1: Die Entwicklung des regionalen Klimamodells REMO; Quelle: http://www.remo-rcm.de/The-Regional-Model-REMO.1267.0.html
Atmosphärische Dynamik und Modellkonfiguration
Die Modellgleichungen werden in einem rotierten sphärischen Koordinatensystem formuliert, das durch Drehungen aus dem geographischen System entsteht. Bei der Rotation wird der Pol so positioniert, dass der rotierte Äquator durch die Mitte des Modellgebietes verläuft. Dies hat den Vorteil, dass die Gitterzellen annähernd quadratisch sind und in ihrer Größe nur wenig variieren, so dass die numerische Lösung der Modellgleichungen einfacher wird. Der horizontale Abstand der Gitterzellen beträgt in der REMO Version mit hydrostatischer Approximation [1] 0.5° bis 0.088°; REMO ohne hydrostatische Annahme (Göttel 2009) wird bis zu einer Horizontalauflösung von 0.011° verwendet.
[1] Die hydrostatische Approximation geht von einem vertikalen Gleichgewicht zwischen Luftdruckgradientkraft und Schwerkraft aus und vernachlässigt damit Vertikalbeschleunigung.
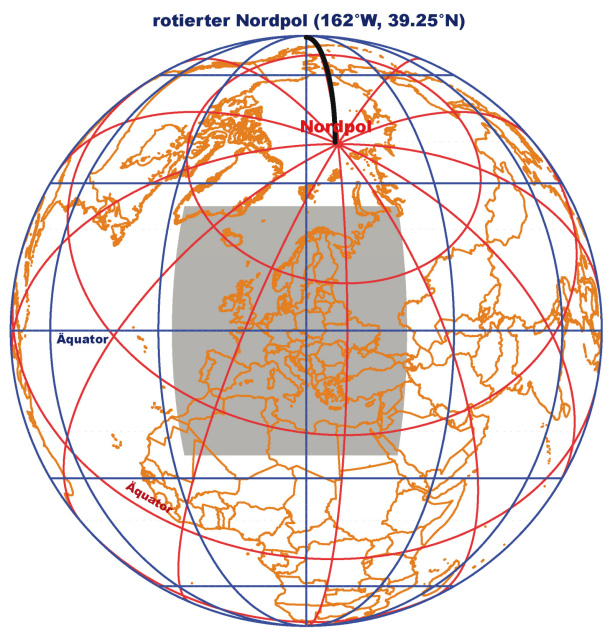
Abbildung 2: Rotiertes sphärisches Koordinatensystem (Göttel 2009)
Die prognostischen Variablen von REMO sind Bodendruck, Temperatur, horizontale Windkomponenten, Wasserdampfgehalt und Flüssigwasser. Zu Beginn der Simulation benötigt das Regionalmodell die Anfangsbedingungen der prognostischen Variablen. Über den Landflächen müssen zudem die Bodentemperaturen und die Bodenfeuchte initialisiert werden. Während der Simulation werden aus einem globalen Datensatz die prognostischen Variablen (Flüssigwasser nur falls vorhanden) als seitliche Randbedingungen in einer zeitlichen Auflösung von 6 Stunden vorgegeben. Diese Daten werden nach dem Randrelaxations-Verfahren von Davies (1976) in einer Randzone von 8 Gitterboxen verwendet, in welcher die extern vorgegebenen mit den intern berechneten Variablen in Einklang gebracht werden.
In der vertikalen Dimension wird ein hybrides Koordinatensystem mit geländefolgenden Modellflächen nach Simmons und Burridge (1981) verwendet. Dabei ist die Vertikalkoordinate eine monotone Funktion des Druckes, und hängt zudem vom räumlich und zeitlich variablen Bodendruck ab; sie beträgt am oberen Rand der Atmosphäre 0 und an der Untergrenze 1. Die Modellflächen folgen in den unteren Schichten der Modellorographie, während die hohen Druckniveaus etwa horizontal verlaufen. In der Mitte zwischen zwei Druckniveaus werden die prognostischen Variablen bestimmt, die damit die gesamte Schicht zwischen zwei definierten Schichtgrenzen repräsentieren. Die horizontalen Windkomponenten sind an den Mittelpunkten der Seitenflächen definiert. Die horizontale Diskretisierung beruht auf einem sogenannten Arakawa-C-Gitter (Arakawa 1988), in dem alle Variablenwerte (außer den Windkomponenten) für das Zentrum der jeweiligen Gitterbox gültig sind.
Die zeitliche Integration der Modellgleichungen in REMO beruht auf dem sogenannten Leapfrog-Schema mit semi-implizierter Korrektur und Zeitfilterung nach Asselin (1972); die Erläuterung dieser Methoden kann in der Dokumentation des EM/DM-Systems des Deutschen Wetterdienstes (DWD 1995) nachgelesen werden. Der Rechenzeitschritt variiert je nach horizontaler Auflösung von etwa 5 Minuten (bei 0.5° Horizontalauflösung) bis 10 Sekunden (bei 0.011° Auflösung).
Zum REMO-Github
Physikalische Parametrisierungen
Die Strahlung wird nach einem Schema von Morcrette (1986) parameterisiert, wobei Modifikationen für zusätzliche Treibhausgase, die 14.6 μm-Bande des Ozons sowie verschiedene Aerosoltypen vorgenommen werden.
Die Konvektionsparameterisierung erfolgt durch das Massenflussschema nach Tiedtke (1989) mit Modifikationen nach Nordeng (1994). Die Parameterisierung nicht-konvektiver Wolken und Niederschlagsbildung erfolgt nach Lohmann und Röckner (1995) und Röckner et al. (1996).
Die Vertikaldiffusion beruht auf der Monin-Obukhov-Theorie (Louis 1979). Die turbulenten Flüsse sind zum Vertikalgradienten der entsprechenden Variablen und zum turbulenten Diffusionskoeffizienten proportional. Die Diffusionskoeffizienten werden als Funktion der turbulenten kinetischen Energie berechnet.
Für die Austauschprozesse zwischen Erdoberfläche und Atmosphäre werden innerhalb einer Gitterzelle die subskaligen Anteile von Land, Wasser und Meereis unterschieden (Semmler 2004). Auf den Landflächen wird zwischen nacktem Boden und vegetationsbedeckten Flächen unterschieden. Der Boden kann hierbei auch teilweise oder ganz schneebedeckt sein. Weiterhin gibt es eine Modellversion, in der auch Eisflächen über Land mittels eines dynamischen Gletscher-Moduls simuliert werden können (Kotlarksi 2007).
Die Eigenschaften der Vegetationsbedeckung werden durch verschiedene Vegetationsparameter für bis zu etwa 70 verschiedene Ökosystemtypen berücksichtigt, die in einer räumlichen Auflösung von etwa 1km x 1km vorliegen (Hagemann 1999, 2002). Die Vegetationsparameter aller in einer Modellgitterzelle vorkommenden Ökosystemtypen werden zu einem mittleren Wert aggregiert. Der Blattflächenindex und der Anteil photosynthetisch aktiver Vegetation variieren zudem im Jahresverlauf (Rechid et al., 2006). Ebenso die Oberflächenalbedo über schneefreien, vegetationsbedeckten Landoberflächen, die als Funktion des Blattflächenindex beschrieben wird (Rechid et al., 2009).
Die Bodenparameterisierung beinhaltet den Wärmetransport in einem 5-Schichten-Modell nach Warrilow et al. (1986) bis zu einer Tiefe von 10 m sowie hydrologische Prozesse in einem "Bucket" - Modell, die auch den Einfluss der Vegetation einbeziehen. Eine kurze Übersicht zu dem Landoberflächenschema in REMO ist unter folgendem Link zu finden:
Land Surface Scheme of REMO
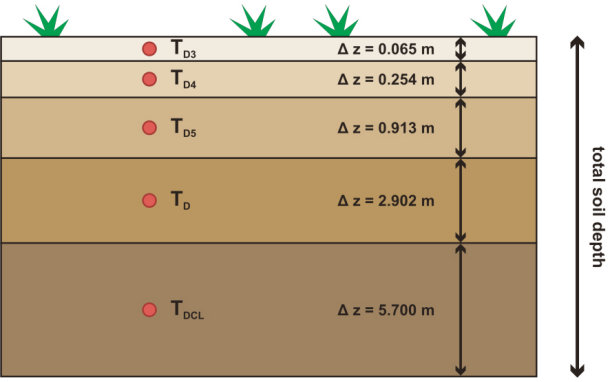
Abbildung 3. 5-Schichtenmodell für Wärmediffusion im Boden in REMO (Kotlarski 2007)
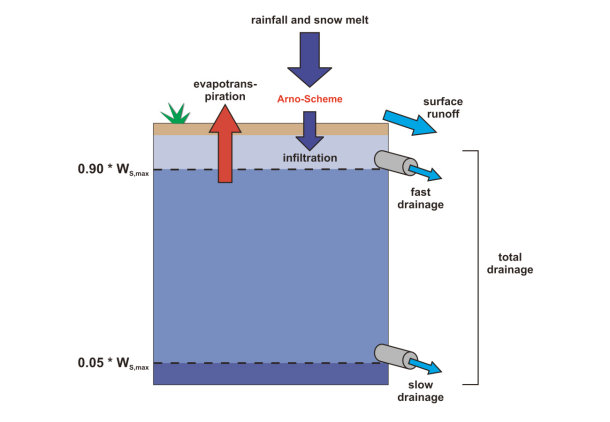
Abbildung 4. 1-"Bucket"-Modell der Bodenhydrologie in REMO (Kotlarski 2007)
Ausgabegrößen
Zu den berechneten Ausgabegrößen gehören die prognostischen Variablen Temperatur, horizontale Windkomponenten, spezifische Feuchte und Wolkenwasser; diese werden für alle Atmosphärenlevel in dreidimensionalen Feldern in einem zeitlichen Intervall von 6 Stunden ausgegeben. Die zweidimensionalen Größen, wie z.B. bodennahe Lufttemperatur, Niederschlag, Verdunstung, Stahlung oder Wolkenbedeckungsgrad werden stündlich abgespeichert.
Dr. Diana Rechid
Climate Service Center Germany (GERICS)
- Arakawa A (1988) Finite-Difference Methods in Climate Modeling. Proceedings of the NATO Advanced Study Institute on Physically-Based Modeling and Simulation of Climate and Climate Change (Part 1), Erice, Italy, 11-23 May 1986
- Asselin R (1972) Frequency Filter for Time Integrations. Mon. Wea. Rev., 100, 487–490
- Davies H C A (1976) Lateral boundary formulation for multi-level prediction models. Quart. J. R. Meteor. Soc. 1976, 102, 405–418
- DWD (1995) Dokumentation des EM/DM-Systems. Deutscher Wetterdienst. Zentralamt. Abteilung Forschung und Entwicklung, Offenbach am Main
- Hagemann S (2002) An improved land surface parameter dataset for global and regional climate models. Report 336, Max-Planck-Institute for Meteorology, Hamburg
- Hagemann S, Botzet M, Dümenil L, Machenhauer M (1999) Derivation of global GCM boundary conditions from 1 km land use satellite data. Report 289, Max-Planck-Institute for Meteorology, Hamburg
- Jacob D, Podzun R (1997) Sensitivity studies with the regional climate model REMO. Meteorology and Atmospheric Physics, 63 (1-2), 119-129
- Jacob D (2001) A note to the simulation of the annual and inter-annual variability of the water budget over the Baltic Sea drainage basin. Meteorology and Atmospheric Physics, 77 (1-4), 61-73
- Kotlarski S (2007) A Subgrid Glacier Parameterisation for Use in Regional Climate Modelling. Berichte zur Erdsystemforschung, 42, Max-Planck-Institute for Meteorology, Hamburg
- Lohmann U, Roeckner E (1995) Introduction of a prognostic cloud ice scheme in the ECHAM general circulation model: Impact on climate and climate sensitivity. Max-Planck-Institut für Meteorologie, Report No. 179
- Louis J-F (1979) A parametric model of vertical eddy fluxes in the atmosphere. Boundary-Layer Meteor., 17, 187-202
- Majewski D (1991) The Europa-Modell of the Deutscher Wetterdienst. ECMWF Seminar on Numerical Methods in Atmospheric Models, 2, 147-191
- Arakawa A (1988) Finite-Difference Methods in Climate Modeling. Proceedings of the NATO Advanced Study Institute on Physically-Based Modeling and Simulation of Climate and Climate Change (Part 1), Erice, Italy, 11-23 May 1986
- Asselin R (1972) Frequency Filter for Time Integrations. Mon. Wea. Rev., 100, 487–490
- Göttel H (2009) Einfluss der nichthydrostatischen Modellierung und der Niederschlagsverdriftung auf die Ergebnisse regionaler Klimamodellierung. Berichte zur Erdsystemforschung, 60, Max-Planck-Institute for Meteorology, Hamburg
- Hagemann S, Botzet M, Dümenil L, Machenhauer M (1999) Derivation of global GCM boundary conditions from 1 km land use satellite data. Report 289, Max-Planck-Institute for Meteorology, Hamburg
- Jacob D, Podzun R(1997) Sensitivity studies with the regional climate model REMO. Meteorology and Atmospheric Physics, 63 (1-2), 119-129
- Jacob D (2001) A note to the simulation of the annual and inter-annual variability of the water budget over the Baltic Sea drainage basin. Meteorology and Atmospheric Physics, 77 (1-4), 61-73
- Louis J-F (1979) A parametric model of vertical eddy fluxes in the atmosphere. Boundary-Layer Meteor., 17, 187-202
- Majewski D (1991) The Europa-Modell of the Deutscher Wetterdienst. ECMWF Seminar on Numerical Methods in Atmospheric Models, 2, 147-191
- Morcrette J-J, Smith L, Fourquart Y (1986) Pressure and temperature dependance of the absorption in longwave radiation parameterizations. Beitr. Phys. Atmos. 59, 455-469
- Nordeng T E (1994) Extended versions of the convective parametrization scheme at ECMWF and their impact on the mean and transient activity of the model in the tropics. ECMWF Research Department, Technical Momorandum No. 206, October 1994, 41 pp, European Centre for Medium Range Weather Forecasts, Reading, UK
- Rechid D, Jacob D (2006) Influence of monthly varying vegetation on the simulated climate in Europe. Meteorologische Zeitschrift, 15, 99-116. doi: 10.1127/0941-2948/2006/0091
- Rechid D, Raddatz T J, Jacob D (2009) Parameterization of snow-free land surface albedo as a function of vegetation phenology based on MODIS data and applied in climate modelling. Theor. Appl. Climatol. 95, 245–255
- Roeckner E. Arpe K, Bengtsson L, Christoph M, Claussen M, Dümenil L, Esch M, Giorgetta M, Schlese U, Schulzweida U (1996) The atmospheric general circulation model ECHAM-4: Model description and simulation of present-day climate. Report No. 218, Max-Planck-Institute for Meteorology, Hamburg
- Semmler T, Jacob D, Schlünzen KH, Podzun R (2004) Influence of sea ice treatment in a regional climate model on boundary layer values in the Fram Strait region. Mon Weather Rev, 132, 985-999
- Sundquist H (1978) A parameterization scheme for non-convective condensation including precipitation including prediction of cloud water content. Quart. J. R. Met. Soc., 104, 677-690.
- Tiedtke M (1989) A comprehensive mass flux scheme for cumulus parameterization in large scale models. Mon. Wea. Rev., 117, 1779-1800.
- Warrilow DA, Sangster AB, Slingo A (1986) Modelling of land surface processes and their influence on European climate. Meteorological Office, Met O 20 Technical Note DCTN 38, Backnell, UK